La forme de la Terre, d'Aristote aux satellites géodésiques

Daniel Raymond


Daniel Raymond, ancien maître de conférences à l'Université Pierre et Marie Curie est un habitué de nos réunions. Aujourd'hui, le sujet de son exposé La forme de la Terre, d'Aristote aux satellites géodésiques, est un peu particulier pour la SAGA puisqu'il ne traite pas de Géologie, mais de Géodésie, plus précisément de l'histoire de la Géodésie, histoire passionnante et peu connue du grand public.

Introduction

Au IIe siècle av. J.-C., les Grecs savaient que la Terre était ronde et avaient même mesuré son rayon avec une remarquable précision. L'idée s'est ensuite perdue au Moyen-Age avant d'être réintroduite. Au début du XVIIe siècle, Descartes posa la question de la rotondité de la Terre en termes scientifiques, ce fut le début d'une longue controverse qui conclut au siècle suivant que la Terre était aplatie aux pôles et avait la forme d'un ellipsoïde. Plus près de nous, les satellites nous ont donné une géométrie très précise de la Terre permettant de mesurer les écarts par rapport à cet ellipsoïde.

Cette conférence présente les grandes étapes de notre connaissance de la forme de notre planète.

Les conceptions sur la forme de la Terre avant le XVIIe siècle

Les cosmogonies des civilisations très anciennes, chinoise, indienne ou sumérienne, considéraient que la Terre était plate ; l'idée reposait sur la perception par l'Homme de son environnement immédiat et sur des croyances religieuses.

Les premiers philosophes grecs pensaient de même : pour Thalès (625 - 545 av. J.-C.), la Terre était un disque plat posé sur l'eau dont l'agitation épisodique provoquait les séismes. Le premier pas vers la notion de courbure vint d'Anaximandre, un de ses disciples : observant la courbure de l'horizon marin, il émit l'idée d'une Terre ayant la forme d'un cylindre flottant dans un univers infini.

L'idée fut ensuite énoncée par plusieurs philosophes, pas toujours avec des preuves concrètes ; Platon (428 - 348 av. J.-C.) par exemple, pensait que la Terre était une boule parce qu'elle était au centre de l'univers et qu'elle ne pouvait pas avoir une autre forme. Aristote (384 - 322 av. J.-C.) apporta des arguments factuels au raisonnement philosophique :

Quelques années plus tard, Aristarque de Samos (310 - 230 av. J.-C.), reprenant l'hypothèse de la rotondité de la Terre, mit au point une méthode correcte d'évaluation de la distance Terre - Lune et fut le premier à proposer que la Terre tourne autour du Soleil, ce qui d'ailleurs lui valut les foudres des Stoïciens.



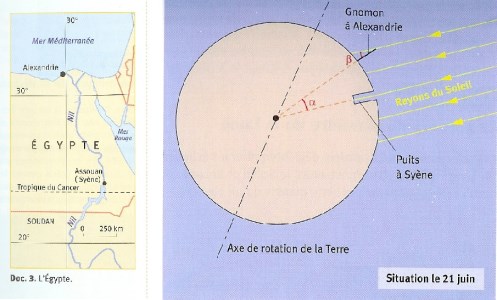L'expérience d'Eratosthène

Mais c'est Eratosthène (environ 276 - 175 av. J.-C.) qui fit faire un progrès décisif à notre connaissance sur la forme de la Terre. On lui doit une carte du monde, et on lui attribue les premières mesures de la circonférence et du rayon de la Terre (sans preuves formelles il est vrai) grâce à une expérience fort ingénieuse :

Plus de 20 siècles après l'expérience, on est impressionné par sa beauté et la précision du résultat, moins de 2% d'erreur !



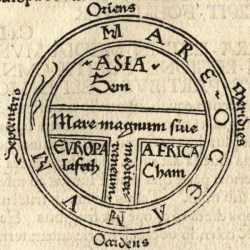Une carte terrarum orbis du Ve siècle

Après ces avancées, le Moyen Age apparaît comme une longue période où la science progresse peu et où l'Eglise se méfie des savants. On peut à titre d'exemple, citer la représentation de la Terre dite en TO (terrarum orbis) : un cercle divisé en trois parties séparées par des bras de mer : en haut, l'Asie et en bas, l'Europe à gauche et l'Afrique à droite. Cette image traduit l'idée d'une Terre ronde, fondée sur les croyances et les interprétations religieuses de l'époque : la Sainte Trinité, le paradis terrestre en Orient, le peuplement de la Terre par les trois fils de Noë. La Renaissance apporta peu de progrès significatifs dans ce domaine, malgré la carte du monde de Léonard de Vinci.

Les XVIIe et XVIIIe siècles, Cassini contre Newton ou les débuts de la géodésie moderne

La naissance de la controverse

Si l'idée d'une Terre sphérique est très ancienne, celle d'une sphère imparfaite est beaucoup plus récente. Descartes (1596 - 1650) posa la question pour la première fois... en se trompant, car il pensait que la rotation de la Terre sur elle-même devait lui donner une forme allongée suivant l'axe des pôles. L'hypothèse fut reprise par deux astronomes directeurs de l'Observatoire de Paris, Jean-Dominique Cassini (1625 - 1712), le découvreur des anneaux de Saturne et son fils Jacques Cassini (1677 - 1756). A la même époque, Isaac Newton (1642 - 1724), avança l'hypothèse contraire : la Terre, fluide lors de sa formation, avait acquis sous l'effet de la force axifuge, la forme d'un ellipsoïde aplati aux pôles.

Ainisi naquit une âpre controverse scientifique. Qui avait raison ?



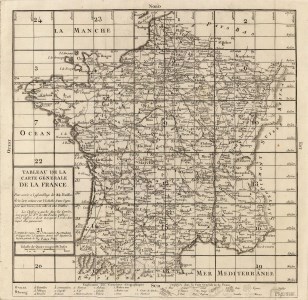Carte de France de Cassini

Les débuts de la géodésie géométrique

La querelle entre Cassiniens et Newtoniens coïncida avec une préoccupation pratique de l'époque, celle d'avoir une carte de France précise. Sur ordre de Louis XIV, Colbert chargea en 1683 l'Académie des Sciences de s'attaquer à cette tâche qui fut confiée aux Cassini père et fils.

Les Cassini utilisèrent la technique de triangulation et arpentèrent le méridien de Paris, du Canigou à Paris et de Paris à Dunkerque. En mesurant les latitudes des lieux arpentés (par visée d'une même étoile), ils pouvaient calculer la courbure de la Terre, du moins, celle correspondant au nord et au sud de la France. Leurs résulats donnaient un allongement du globe selon les pôles, et confirmaient la thèse de Descartes... ce qui devait s'avérer faux par la suite.

La triangulation des Cassini n'était pas assez précise pour le but qu'elle s'était fixée, mais a été suivie par d'autres opérations qui ont eu un intérêt scientifique majeur, notamment celle de Delambre et Méchain qui permit la mesure d'un arc de méridien entre Dunkerque et Barcelone et a servi à la première définition du mètre, la dix millionième partie du quart du méridien terrestre.

Les débuts de la géodésie gravimétrique

Les lois de la gravitation universelles ont été formellement comprises par Newton. Appliquées à la gravitation terrestre, elles expriment que la chute des corps à la surface de la Terre est uniformément accélérée, l'accélération de la pesanteur étant donnée par la formule g = G . M / R2

Une autre formule élémentaire, celle de la période d'oscillation du pendule, fait intervenir l'accélération de la pesanteur T = 2 . Π . (L/g)1/2

Le rapprochement des deux formules permet de comparer les rayons terrestres en différents lieux en mesurant les périodes d'oscillation des pendules en ces lieux, et Jean Richer, astronome et horloger, fit en 1672 l'expérience suivante à Paris, puis à Cayenne :

Cayenne étant proche de l'équateur, l'augmentation de la période du pendule traduisait une diminution de g, donc un renflement du globe à l'équateur et d'un aplatissement aux pôles. L'expérience, en contradiction avec celle des Cassini, validait l'hypothèse de Newton.

Les expéditions de Laponie et du Pérou

Pour mettre fin à la querelle, Louis XV commandita deux expéditions pour mesurer un arc de méridien par triangulation, d'une part dans les régions polaires, d'autre part à l'équateur.

L'expédition en Laponie eut lieu en 1736 et fut dirigée par deux scientifiques réputés, Pierre-Louis Moreau de Maupertuis (1698 - 1759) et Claude Clairaut (1713 - 1765), acompagnés par le physicien suédois Anders Celsius. Ils firent les mesures dans la région de Tornio, à la frontière actuelle entre la Finlande et la Suède. Au bout d'un an, l'expérience était terminée et montrait qu'à cette latitude, un arc de méridien de 1° était plus grand qu'il ne l'aurait été dans le cas d'une Terre parfaitement sphérique. Elle confirmait donc l'hypothèse de Newton, ce que Voltaire résuma en deux vers peu amènes pour les savants français

« Vous êtes aller chercher en ces lieux pleins d'ennui
Ce que Newton trouva sans sortir de chez lui »

L'expédition au Pérou dura beaucoup plus longtemps, de 1735 à 1743. Elle était dirigée par le mathématicien Louis Godin (1704 - 1760) et comprenait entre autres le mathématicien et astronome Pierre Bouguer (1698 - 1731), le géographe Charles de la Condamine (1701 -1774) et le botaniste Joseph de Jussieu (1704 -1779). L'expédition rencontra de nombreuses difficultés (problèmes politiques, logistiques, financiers, de santé et de sécurité) et la mésentente entre les participants n'arrangea rien. Au bout de huit ans, les mesures étaient faites et confirmaient les résultats de la mission lapone, ce qui mettait fin à la querelle Newtoniens / Cassiniens qui avait duré une soixantaine d'années.

Ces missions permirent de calculer le coefficient d'aplatissement de la Terre, soit 1/298 et de définir l'ellipsoïde référence, forme théorique de la Terre. Clairaut, père de la mécanique des fluides, en déduisit que la Terre se comporte non comme un fluide homogène mais comme un solide élastique.



Une représentation du géoïde

Le facteur d'amplification des hauteurs est de 15 000
Source : International Centre for Global Earth Models

De l'ellipsoïde de référence à la forme réelle de la Terre, ou géoïde

Lorsque l'ellipsoïde de référence a été défini, on a cherché à le comparer à la surface réelle de notre globe. A partir de l'ellipsoïde, on peut calculer la valeur de g en chaque point de la Terre en fonction de sa latitude et la comparer avec la valeur mesurée, mesure effectuée autrefois avec un pendule, de nos jours avec un gravimètre :

On s'est rapidement rendu compte qu'en de nombreux points du globe, les valeurs calculées n'étaient pas égales à celles des mesures. Autrement dit, l'ellipsoïde de référence n'était pas une très bonne représentation de la Terre.

Pour améliorer le modèle, on a défini le géoïde comme étant la surface équipotentielle du champ de gravité proche du niveau moyen des océans. On peut démontrer qu'en tout point du globe, cette surface est perpendiculaire au fil à plomb. Les écarts entre l'ellipsoïde de référence et le géoïde viennent des défauts d'homogénéité du globe :

La géodésie aujourd'hui, l'apport des satellites

Principe de la caractérisation du géoïde par les satellites géodésiques

En fait, avant 1960, la forme du géoïde était mal connue car elle nécessitait de nombreuses mesures avec des gravimètres ; l'utilisation des satellites géodésiques a permis d'établir un géoïde beaucoup plus précis. Ces satellites se déplacent sur des orbites quasi circulaires situées sur une surface équipotentielle de pesanteur, parallèle au géoïde. A chaque rotation, ils survolent une nouvelle région du globe et ne retrouvent leur première révolution qu'au bout d'un certain temps appelé cycle orbital.

Le principe de la détermination du géoïde est le suivant :

Mise en évidence des anomalies à grande longueur d'onde du géoïde

Les résultats obtenus par les satellites géodésiques sont spectaculaires à l'échelle du millier de kilomètres. Le géoïde montre des des écarts par rapport à l'ellipsoïde, négatifs (creux) ou positifs (bosses). Les écarts les plus importants sont - 104 mètres dans l'Océan indien et + 86 mètres en Nouvelle Guinée. Finalement, le géoïde est représenté par une surface relativement irrégulière, du moins, qui paraît telle, lorsqu'on amplifie l'échelle des altitudes.

Mais il faut noter que l'interprétation de ces résultats est controversée car les écarts résultent de phénomènes pouvant jouer en sens opposés. Exemple :




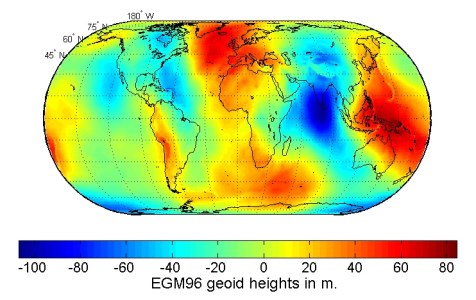Ecarts en mètres entre le géoïde et l'ellipsoïde de référence

Source : Wikimedia Commons, NASA

Du géoïde au relief terrestre, l'apport des satellites altimétriques radar

Les satellites géodésiques ne permettent pas de détecter les anomalies fines du géoïde. Un progrès décisif a été effecué avec l'altimétrie satellitaire radar, technique utilisée depuis une vingtaine d'années pour étudier les fonds océaniques : le principe consiste à mesurer de façon très précise le trajet aller / retour d'une très brève impulsion radar envoyée vers la Terre perpendiculairement à la trajectoire du satellite. Comme pour les satellites géodésiques, on mesure les écarts entre la trajectoire réelle du satellite et l'ellipsoïde de référence.

Les résultats obtenus avec cette technique font apparaître de nouvelles anomalies par rapport à l'ellipoïde de référence. Ces anomalies, positives ou négatives, sont de l'ordre de quelques mètres sur des distances de quelques dizaines de kilomètres seulement et on a constaté la relation avec la topographie sous-marine : un relief au fond de l'océan provoque un soulèvement de la surface océanique et une dépression provoque l'effet inverse.

Cette méthode a permis des progrès importants dans notre connaissance du relief des fonds océaniques. Les grandes dorsales océaniques de 2 000 à 4 000 mètres d'altitude sont marquées par une bosse de l'ordre de 20 mètres sur le géoïde, les fosses, qui pouvent aller jusqu'à 11 000 mètres de profondeur se traduisent par des creux du même ordre de grandeur.

Pour conclure, on peut dire que plusieurs missions satellitaires sont récentes ou en cours (CHAMP, GOCE, GRACE) parce que les applications pratiques du géoïde sont nombreuses :

Ces perspectives sont de toute évidence très loin de la Terre sphérique d'Aristote...

Après les questions des participants, il ne nous reste qu'à remercier amicalement Daniel Raymond pour cette conférence qui nous a permis de découvrir un bel exemple de l'histoire des Sciences. Nous espérons le revoir prochainement sur d'autres sujets.

Quelques liens internet et documents sur le thème de la conférence :